Thứ Sáu, 2 tháng 5, 2014

Cạm bẫy trong xác suất - Phần 1. Cạm bẫy của các Đấng Tối Cao.

   
Có thể bạn quan tâm



  Bài viết tại http://vietsciences.free.fr

Phần 1. Cạm bẫy của các Đấng Tối Cao.

♠. Chữ tình chữ hiếu, chữ nào trọng hơn?
Có một báo treo giải cho câu đố xã hội như thế này: “Vua, cha và thầy đi cùng thuyền với ta. Đến giữa sông, thuyền bị chìm. Người duy nhất biết bơi là ta. Ta phải cứu ai trước?”. Quả là khó khăn. Giải thưởng được trao cho cậu bé 12 tuổi. Cậu trả lời: “Cứu người gần mình nhất.”. Nghĩ lại, thấy thật là có lý. Cứu người gần mình nhất thì xác suất thành công cao hơn (với điều kiện khoảng cách giữa mọi người rất nhỏ so với khoảng cách từ họ đến bờ). Và xác suất cứu xong, quay trở lại để cứu người thứ hai cũng cao. Thế nhưng, nếu cậu bé vào tuổi 21 và có vợ, còn đề ra như thế này: “Nữ hoàng, mẹ và vợ đi cùng thuyền với ta. Đến giữa sông, thuyền bị chìm. Người duy nhất biết bơi là ta. Ta phải cứu ai trước?”, chắc cậu chả dại dột gì trả lời câu như vậy đâu. Còn mấy ông giám khảo mà chấm câu đấy giải nhất cũng liệu cái thần hồn.
Thượng đế đã sinh ra Adam. Thấy chàng buồn, bèn lấy xương sườn của chàng làm ra nàng Eva xinh đẹp. Để rồi một hôm, nàng nghe lời xui dại của con rắn (hình như trong Kinh Thánh không nói con rắn này là đực hay cái) ăn quả cấm. Nàng quyến rũ anh khờ Adam sa ngã theo. Họ chơi trò chơi Ái Tình. Họ mãi mê đến nỗi Thượng Đế bực dọc và đuổi họ ra khỏi Thiên Đàng. Có phải chăng Ái Tình là thứ tình cảm đầu tiên của giống Người chúng ta?!. Đầu Tiên và Trường Tồn nhất. Và đến một ngày xa tít của thế kỷ 21, một anh chàng đứng trước chữ Tình và chữ Hiếu không biết chọn cái gì, đành phải phó thác cho Thượng Đế:
Mỗi lần đi chơi, anh chàng muốn hoặc đi về nhà mẹ hoặc đi tới nhà người yêu. Mẹ và người yêu anh ta ở hai hướng khác nhau của con đường (anh ta ở giữa). Anh ta thường phân vân không biết về đâu. Cuối cùng, anh ta chọn được giải pháp thích hợp: hễ có xe buýt hướng nào trước, thì đi về hướng ấy. Xe buýt của cả hai hướng cứ 15’ có một chuyến. Sau một năm, anh ta tổng kết lại thì phát hiện số lần đi về nhà người yêu lớn gấp hai lần số lần về với mẹ. Anh chàng  sung sướng: “Ái tình, Ái tình…Quả không sai người ta gọi ngươi là đề tài muôn thuở của con người. Thượng đế thật là tâm lý. Chính Ngài đã xui khiến cho ta chọn chữ Tình nhiều hơn.”.
Khi nghe câu chuyện trên, một cô bạn của tôi đã reo lên: “Thế mà em chả biết cách chọn này. Vừa đúng em có hai ý trung nhân ở giữa hai đầu đường. Em chả biết đi lại thế nào cho phải đạo nữa.”. Tôi nói: “Từ từ nào…Nhưng thôi, cứ theo cách đấy. Sau ít lâu về thông báo cho tôi biết kết quả ra sao.”. Bẵng đi một dạo, cô tiu nghỉu bảo với tôi: “Anh ạ, cái anh chàng em không ưa lắm thì em phải đi đến gấp năm lần anh kia. Thượng Đế quả là bên trọng bên khinh.”.
Thực ra, từ khi Thượng Đế đuổi Adam và Eva xuống thế gian này thì Ngài đã phó thác Ái Tình cho Trái Tim của Con Người rồi. Còn… giải thích hai hiện tượng trên phải dùng xác suất mới xong.Các bạn hãy theo dõi hình sau:


Xe buýt đi về hướng mẹ bắt đầu từ lúc 6:00 sáng và cứ cách 15’ có một chuyến theo lịch: 6:00, 6:15, 6:30, 6:45, 7:00…Còn xe buýt đi về hướng nhà người yêu lại có đầu tiên lúc 6:10 và cách 15’ có một chuyến theo lịch: 6:10, 6:25, 6:40, 6:55, 7:10…Theo dõi trên hình, chúng ta thấy, nếu chàng trai đi vào những thời điểm ngẫu nhiên thì thời gian anh ta đợi được xe buýt về hướng người yêu gấp đôi thời gian về hướng mẹ. Từ 6:00 đến 6:10 anh ta đợi chuyến đến người yêu (10’). Từ 6:10 đến 6:15 anh ta đợi chuyến đến nhà mẹ (5’). Suy ra, xác suất anh chàng về hướng người yêu phải gấp hai lần hướng mẹ. Và điều đó đã xảy ra trên thực tế.
Còn trường hợp đối với cô gái, thời gian (ví dụ) các chuyến xe buýt cách nhau 30’. Và chuyến về anh chàng không thích lắm là 6:25, 6:55, 7:25…, chuyến về anh chàng thích là 6:00, 6:30, 7:00…Chuyện cô gái phải ăn quả đắng đi về hướng anh chàng không thích lắm nhiều hơn gấp 5 lần không dính dáng gì đến Thượng Đế cả. Trừ phi, cô nàng thuyết phục hai anh chàng đổi chỗ cho nhau mà kết quả vẫn như trên…Thì… chứng tỏ Thượng Đế đã xui khiến cho công ty xe buýt thành phố đổi lại lịch xe đúng khi hai anh chàng chuyển chỗ cho nhau!!![1]

♣. Thánh nhân đãi kẻ khù khờ?
Một nhà thông thái nghĩ mình đã biết hết mọi việc trên đời. Có lần, ông gặp một bác nông dân trông thật là…nông dân. Quá tự phụ vào kiến thức của mình, ông ta bảo bác nông dân: “Bây giờ, ông hỏi tôi một câu, nếu tôi không trả lời được thì tôi trả ông 10 đồng. Sau đó, tôi hỏi ông một câu, ông không trả lời được, ông trả tôi 1 đồng.”. Bác nông dân “Được, tôi chấp nhận cá cược.”. “Vậy, nhường ông hỏi trước.”, nhà thông thái trả lời. Bác nông dân nói “Tôi xin hỏi ông, con gì chạy xuống núi bằng bốn chân, mà chạy lên núi chỉ bằng ba chân.”. Suy nghĩ mãi, nhà thông thái đành trả lời: “Tôi không biết.”, và rút 10 đồng ra trả. Ông ta bèn hỏi: “Con gì ngộ vậy?”. Bác nông dân rút 1 đồng trả nhà thông thái và nói: “Tôi cũng không biết.”.
Trong cuộc sống thường ngày và ngay cả trong khoa học, chúng ta chứng kiến không biết bao nhiêu trường hợp:
“Ai đời châu chấu đá xe
Tưởng rằng chấu ngã, ai dè xe nghiêng”
như thế…
Trong cuốn Mathematical Puzzles and Diversions, Martin Gardner đã dẫn một ví dụ tuyệt diệu về khả năng chiến thắng kẻ mạnh hơn như sau:
Smit, Brown và John quyết định đấu súng tay ba theo luật sau: đầu tiên họ sẽ bốc thăm xem ai bắn trước, bắn nhì và bắn cuối. Mỗi người đến lượt mình chỉ bắn được một phát và có thể nhắm vào bất kỳ người nào. Cuộc đấu súng tiếp diễn đến khi chỉ còn sống sót một người. Thoả thuận về luật và bốc thăm xong, ba người đứng vào vị trí của mình (là đỉnh của tam giác đều). Cả ba đều biết khả năng hai đối thủ của mình: Smit không bao giờ trượt, Brown bắn trúng đến 80% số lần bắn, còn John thì bắn trượt cũng như bắn trúng(50/50).
Ai sẽ là người có cơ hội sống sót lớn nhất? Biết rằng cả ba đều thực hiện chiến thuật tối ưu nhất. Và kết quả bốc thăm được sử dụng cho cả trận đấu.
Khi tôi giới thiệu bài toán này với những người bạn, tôi đã nhận rất nhiều ý kiến giải đáp khác nhau. Có người cho Smit có khả năng sống sót nhiều hơn, có người cho Brown thoát khỏi hiểm nguy cao nhất. Một trong số ý kiến đó có lý luận sau đáng chú ý: việc bốc thăm sẽ cho cơ hội đồng đều cho cả ba bắn trước. Vậy xác suất của mỗi người được bắn trước là 1/3. Ta xét xem xác suất sống sót của mỗi người:
Trường hợp 1: xác suất 1/3, Smit bắn trước. Chiến thuật tối ưu của anh ta: bắn vào Brown. Anh ta hạ Brown, lúc đó John sẽ bắn vào chàng ta với xác suất trúng đích là 50%. Nếu trật (cũng với xác suất 50%) thì Smit sẽ kết liễu John. Vậy với trường hợp này xác suất của anh chàng thiện xạ được sống sót là 1/3 x 1/2 = 1/6. Xác suất sống sót của John là 1/6 và của Brown bằng 0.
Trường hợp 2: xác suất 1/3, Brown bắn trước. Chiến thuật tối ưu của anh ta: bắn vào Smit (xem hình 2). Nếu hạ thủ được Smit với xác suất 4/5, thì xác suất đấu trực tiếp của anh ta với John khi John bắn trước là 4/9 đọ 5/9 (nếu Brown bắn trước sẽ là 8/9 đọ 1/9). Như thế, theo hướng này xác suất John sống sót là 1/3 x 4/5 x 5/9= 4/27, Brown sống sót là 1/3 x 4/5 x 4/9 = 16/135. Nếu không hạ được Smit với xác suất 1/5 thì mỗi người Smit và John có xác suất ½ để bắn tiếp theo. Và theo biểu đồ, chúng ta có thể tính toán cho trường hợp này xác suất sống sót của từng người là:
Smit: 1/60 + 1/120 =1/40
John: 1/540 +1/60 + 1/120 + 4/27=7/40
Brown: 8/540 + 16/135=2/15
(Cộng tất cả các số này lại với nhau sẽ được 1/3)
Trường hợp 3: John bắn trước với xác suất 1/3. Theo hình 3 ta có thể tính được như sau:
Smit: 1/24 + 1/120 =1/20
John: 1/24 +1/120 + 1/54 + 1/27=19/180
Brown: 4/27 + 4/135=8/45
(Cộng tất cả các số này lại với nhau sẽ được 1/3)
Như thế xác suất sống sót của mỗi người là:
Smit: 1/6 +1/40 + 1/20=29/120 =0.242
John: 1/6 + 7/40 + 19/180 =161/360 =0.447
Brown: 2/15 + 8/45 = 14/45=0.311
Rõ ràng, cách tính trên đã chọn cách tối ưu cho cả ba người là: Khi còn hai đối thủ, người bắn nhằm vào kẻ bắn giỏi hơn. Lúc đó, nếu cơ may đối thủ bị bắn chết thì người bắn vào mình sẽ là tay amatơ hơn. Và cơ hội sống nhiều hơn. Lý luận này đã đúng chưa? Hoá ra, anh chàng thiện xạ có xác suất sống còn thấp nhất. Nhưng các bạn hãy chú ý một điểm rất nhỏ thôi, nhưng cũng đánh gẫy toàn bộ lý luận trên đây. Nếu xét việc bắn trước là một cơ hội tốt của người bắn để thoát hiểm, chúng ta thấy điều này chỉ đúng với Smit. Ngược lại, không đúng cho John và Brown (cái xác suất sống sót của Brown tăng lên vì do John chọn sai chiến thuật tối ưu). Khi John bắn trước, nếu sử dụng cách này xác suất sống còn của anh ta là 19/180 đối với 1/6 và 7/40 khi Smit và Brown bắn trước tương ứng. Vậy việc gì John phải bắn vào ai đó, bởi vì bất kỳ người nào bắn tiếp theo (vẫn còn ba người) thì xác suất sống còn của John vẫn cao hơn khi anh ta nhắm vào người khác mà bắn? Chiến thuật tối ưu của John là bắn lên trời. [2] Ngoài những con số ở trên, chúng ta thấy John sử dụng phương thức này để tận dụng cho hai đối thủ mạnh loại trừ nhau. Quan trọng nhất, theo đúng luật khi một đối thủ của John bị loại thì người bắn trước lại là John. Và trong bất kỳ trường hợp nào, anh ta cũng có xác suất hơn ½ sống sót. Chiến thuật tối ưu của Smit đã rõ, anh ta phải bắn vào Brown. Còn Brown cũng vậy, biết rằng John sẽ ngư ông đắc lợi mà bắn vào John không được. Chỉ còn cách bắn vào Smit để tăng cao xác suất sống còn mình lên. Từ những lý luận trên, chúng ta có thể thiết lập biểu đồ xác suất cho cả ba xạ thủ như hình 4:
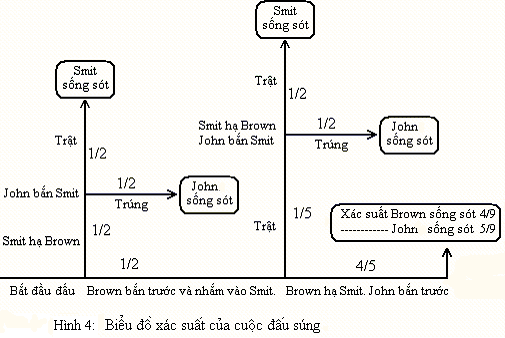
Xác suất cho mỗi người Brown và Smit bắn trước là ½ (Khi còn ba người John là outsider, không tính đến vì anh ta không bắn vào ai cả). Và diễn biến tiếp theo có thể dễ nhận thấy theo hình vẽ. Xác suất của ba người được tính như sau:
Smit: 1/2 x 1/2 + 1/2 x 1/5 x 1/2 = 3/10
Brown: 1/2 x 4/5 x 4/9 = 8/45
John: 1/2 x 1/2 + 1/2 x 1/5 x 1/2 + 1/2 x 4/5 x 5/9 = 47/90
Như vậy chúng ta thấy một “nghịch lý” như sau: John-người bắn kém nhất lại có cơ may sống sót hơn cả cơ may của hai anh chàng bắn giỏi cộng lại. Có phải chăng thánh nhân đãi kẻ khù khờ hay là điều kỳ diệu của xác suất.[3]
 ♥.  Lời an ủi của Diêm Vương?
Ngọc Hoàng Thượng Đế thức giấc, Ngài phóng mắt khắp cõi dương gian và địa ngục xem thần dân của mình ra sao. Đến cửa địa ngục, Ngài thấy ba linh hồn Ghost, Ma và Quái đang xếp hàng chờ đến lượt nhập hộ khẩu. Có lẽ đêm hôm qua, Ngài không gặp ác mộng, nên trong lòng  khoan khoái muốn mở lượng từ bi. Ngài quyết định hồi dương một trong ba linh hồn tội lỗi kia. Ngài bèn sai Nam Tào, Bắc Đẩu viết tên ba linh hồn lên ba tờ giấy và đảo kỹ. Sau đó, Ngài bốc một tờ đưa cho Nam Tào:
-Đây là tên linh hồn được quay về dương gian. Các ngươi mau gõ dây thép xuống cho Diêm Vương được biết!
-Dạ, tuân lệnh.
Đang yên giấc nồng, nhận được điện khẩn từ Thiên Đình, Diêm Vương vội tỉnh ngủ, sửa sang lại cân đai áo mão cho vời ba linh hồn Ghost, Ma, Quái  đến và phán rằng:
-Trong số các ngươi, có một người sẽ được quay về dương gian. Mau chuẩn bị tinh thần sẵn sàng mà hồi dương.
-Chà…
Ba linh hồn quay ra, Diêm Vương thấy Ma còn lần chần không dứt bèn hỏi:
-Nhà ngươi còn chuyện gì không?
-Dạ, thưa Diêm Vương anh minh! Chắc Ngài không muốn chỉ ra ai trong chúng con được quay về. Con chỉ xin Ngài ân huệ nhỏ.
-Được! Ngươi cứ nói.
-Nếu như một trong hai linh hồn kia  được tha về thì Ngài nêu ra tên người ngược lại. Nếu con được tha về thì Ngài có thể nêu bất kỳ tên một trong hai linh hồn kia.
Diêm Vương suy nghĩ một lúc, và nói:
-Thôi được, có một điều an ủi cho ngươi, đó là Quái.
Linh hồn Ma quay về, thấy khoan khoái trong lòng vì nghĩ mình đã lỡm được Diêm Vương. Bởi vì, bây giờ chỉ còn một trong hai người Ghost và Ma được hồi dương. Vậy xác suất hồi dương của mình là ½. Bỗng dưng khi chưa hỏi, thì xác suất hồi dương là 1/3, bây giờ lên được ½ sướng quá còn gì. Còn Diêm Vương thì lẩm bẩm: “Đúng là ngốc tử! Hắn cứ tưởng ta cho hắn một niềm an ủi…”.
Thế thì xác suất được hồi dương của Ma là bao nhiêu?

Thực ra, xác suất của Ma vẫn bằng 1/3. Lúc ban đầu khi Ngọc Hoàng Thượng Đế chọn tên để hồi dương một cách ngẫu nhiên như thế, nên xác suất được hồi dương ban đầu của cả ba là 1/3. Đến lượt Diêm Vương thì nhóm ba người này được chia thành hai nhóm nhỏ. Nhóm thứ nhất là Ma, nhóm thứ nhì gồm cả Ghost và Quái với xác suất tương ứng là 1/3 và 2/3. Theo điều kiện của Ma, Diêm Vương chọn giữa một trong hai người Ghost và Quái một người không được hồi dương. Xác suất Diêm Vương chọn được bằng 1 và không ảnh hưởng gì đến xác suất từng nhóm. Và khi Diêm Vương lộ tẩy bất kỳ một người nào trong nhóm hai thì xác suất nhóm hai và nhóm một không thay đổi. Có nghĩa xác suất của Ma vẫn bằng 1/3 còn xác suất của Ghost được tăng lên thành 2/3 bởi vì xác suất của Quái đã bằng 0.
Để dễ hiểu ta(người chia bài) chọn ba con bài Át Cơ, Át Rô và Át Bích chia cho ba người A, B, C. Xác suất của mỗi người nhận được Át Bích khi chia xong (hay khi chưa lật con nào cả nhưng mỗi con bài đã an vị cho mỗi người) là 1/3. Bây giờ, ta chia ra hai nhóm: nhóm có mỗi A và nhóm có con bài của hai người B, C. Rõ ràng nhóm của hai người B, C có xác suất có con Át Bích bằng 2/3. Nhìn hai lá bài của B, C và chọn ra lá khác Át Bích lật ra (xác suất bằng 1). Điều này hoàn toàn không làm ảnh hưởng đến xác suất của hai nhóm. Duy chỉ có điều, nhóm hai bây giờ chỉ còn một người và xác suất của anh ta tăng gấp đôi bằng 2/3. Trong khi đó nhóm 1 xác suất của A không đổi bằng 1/3.[4]
Ta lại tự đặt cho mình hai tình huống nữa:
-Sau khi chia bài ta rút một con bài nào đó và lật ra. Nếu con bài đó không phải Át Bích thì xác suất của hai người còn lại bằng bao nhiêu? Trường hợp này, ta hoàn toàn không chọn gì cả và xác suất con bài bị lật là Át Bích vẫn bằng 1/3. Lúc này, ba con bài vẫn nằm trong một nhóm tính xác suất đồng nhất và bằng 1. Khi lật lá bài kia ra và phát hiện không phải Át Bích, xác suất của nhóm vẫn bằng 1, nhưng vì hai phần bài còn lại hoàn toàn tương đương nhau trong nhóm nên xác suất của chúng trở thành ½.
-Sau khi chia bài, ta lại cầm lấy cả ba và lật một con bài không phải Át Bích ra. Lý luận tương tự trên ta cũng sẽ thấy xác suất của mỗi tay bài còn lại là Át bích bằng ½.
Hai trường hợp này có xác suất giống nhau và lý luận cũng giống nhau, vậy tại sao phải chia thành hai trường hợp??? Trường hợp nhất, ta cùng ba người chơi phó mặc cho số phận khi lật con bài kia ra. Cái reo vui của hai anh chàng còn lại vì được tăng xác suất đổi bằng cái sầu thảm của anh thứ ba. Và anh thứ ba không trách ta không kéo dài thời gian vui thêm một lúc. Việc ban phát buồn vui là của Thượng Đế. Trường hợp hai, chính ta chọn và ta lại ban cho hai anh này một niềm vui ngắn ngủi còn anh thứ ba một nỗi buồn. (nếu như có con Át Bích sẽ được 1000$ chẳng hạn). Việc ban phát buồn vui là việc của ta.[5]
  
[1]. Cũng không cần thiết hai đầu đường. Nếu như một bến xe buýt có các số 01 chạy về nhà mẹ, 02 chạy về nhà cô giáo, 03 chạy về Nữ Hoàng và 04 chạy đến với người yêu, ta vẫn thiết lập được lịch trình và tính xác suất cụ thể cho từng trường hợp.
[2]. Có người nói, nếu lý luận trên thì ai cũng chờ cho hai đối thủ của mình sát hại lẫn nhau, rồi đến lượt mình bắn chết người còn lại. Điều này đúng nhưng không dành cho Smit vì anh ta là người bắn trăm phát trăm trúng và đây là cuộc đấu súng nên anh ta không thể nhắm vào cột điện mà bắn được. Anh ta phải hạ sát người nào đó khi đến lượt. Và dẫn tới Brown cũng phải bắn vào Smit nếu có lượt trước Smit.
[3]. Những lý luận trên có thể sẽ không đúng với trường hợp 4 hay nhiều hơn người. Chẳng hạn có cuộc đấu súng tay tứ và thêm anh chàng Holmes nào đấy với xác suất bắn trúng là 40%...thì xác suất sống sót mỗi người hoàn toàn khó tính. Vấn đề rất quan trọng là khi đấy, ta gặp một vòng lẩn quẩn. Tìm chiến thuật tối ưu xong tính xác suất. Nhưng khi tính toán xong ta mới nhận ra chiến thuật tối ưu như thế nào. Vì lẽ này, người giải cần tính toán tất cả các khả năng xảy ra và vạch ra chiến thuật tối ưu cho từng người. Một việc làm không dễ dàng. Mời quý vị độc giả thử xem.
[4]. Ta có thể làm cho rõ hơn nữa qua ví dụ sau: Giả sử bốc được lá bài Át Bích sẽ được thưởng 1000$. Có một bộ bài Tây 52 lá, người A rút một lá vậy xác suất anh ta nhận được Át Bích bằng 1/52. A chưa lật bài ra, ta chọn trong 51 lá còn lại 50 lá không phải Át Bích lật ra. Vậy, xác suất của A có lá bài Át Bích là ½ chăng?! Hiển nhiên không đúng. 51 lá còn lại có xác suất là 51/52. Và vì lúc nào ta có thể tìm 50 lá trong 51 khác Át Bích nên chuyện lật hay không lật ra không ảnh hưởng đến xác suất hai nhóm. Ví thế A vẫn có xác suất 1/52 còn lá bài còn lại có xác suất là 51/52.
[5]. Tất cả những trường hợp trên đều là những bài toán Đại số của xác suất mà thôi. Có lần, một anh bạn trẻ hỏi tôi: Có một bộ bài 52 lá, anh bốc một lá và chưa xem. Xong tôi bốc một lá, hỏi xác suất lá của tôi là Át Bích bằng bao nhiêu? Anh bạn lý luận: Nếu lá bài của anh là Át Bích thì xác suất của tôi có Át Bích bằng 0. Nếu lá bài của anh không phải là Át Bích thì xác suất lá bài của tôi là Át Bích bằng 1/51. Vậy tại sao xác suất  lá bài của tôi là Át Bích bằng 1/52? Thực ra, khi nói đến việc bốc lá bài ra người ta nghĩ đến việc trừ những lá bốc rồi (kể cả khi chưa nhìn). Nếu ta xét một bàn quay có 52 ô, tôi đánh dấu một ô cho tôi còn anh bạn kia đánh dấu một ô cho anh ta và quay. Vậy xác suất kim vào đúng ô của tôi hay của anh bạn đều bằng 1/52. Ngoài ra, bản chất xác suất là bình quân các khả năng, ví dụ như trường hợp đấu súng tay ba người ta thấy John bắn trúng cũng như bắn trật. Khi thấy John bắn trúng 3 phát liền, như vậy mấy phát tiếp theo John phải bắn trật. Lý luận này không đúng theo tinh thần xác suất. Xác suất được tính trong một quá trình các trường hợp xảy ra khá nhiều và nó mang ý nghĩa bình quân. Chính vì thế, trở lại câu hỏi anh bạn trẻ, tôi đã trả lời anh ta: có mấy trường hợp tôi bốc con Át Bích-có một với xác suất bạn bốc Át Bích bằng 0. Vậy có mấy trường hợp tôi không bốc được con Át Bích- 51 với xác suất bạn bốc được Át Bích là 1/51. Khi ta chưa biết lá bài của tôi, muốn tính xác suất của bạn, ta phải tính bình quân tất cả các khả năng: (51 x 1/51 + 1 x 0)/52= 1/52.
  




 Dưới đây là quy trình của một cuộc nghiên cứu, bất luận lĩnh vực- quy mô thì nó cũng trải qua đầy đủ các bước

  • B1: Xác định vấn đề nghiên cứu
  • B2: Xác định mục tiêu nghiên cứu
  • B3: Thiết kế dự án- lập kế hoạch
  • B4: Thu thập dữ liệu
  • B5: Kiểm tra
  • B6: làm sạch, mã hóa
  • B7: Phân tích, báo cáo


Trong trường hợp cần chúng tôi hỗ trợ 01 hay nhiều công đoạn- để tạo điều kiện thuận lợi nhất vui lòng gửi toàn bộ các tài liệu liên quan tới các công đoạn trước cho chúng tôi.
***********************************
Các bạn đang xem bài viết tại website XỦ LÝ SỐ LIỆU- Một dịch vụ của Antsmrg
ANTS là nhóm chuyên cung cấp dịch vụ nghiên cứu xã hội- thị trường cho các tổ chức và các nhân ở mọi quy mô. Các dịch vụ của chúng tôi bao gồm
  • Tư vấn, thiết kế nghiên cứu
  • Thiết kế bảng hỏi, thu thập số liệu
  • Phân tích, báo cáo
Đối với dịch vụ XỬ LÝ SỐ LIỆU, chúng tôi cung cấp các gói dịch vụ liên quan
Mọi yêu cầu, thắc mắc vui lòng gửi lại thông tin cho chúng tôi tại mục "Liên hệ với chúng tôi" tại cuối website này.
+++++++++++++++++++++++++++++++